Méthode de l'inversion approchée

Derrière cette notion d'inversion approchée se trouve un concept pour le développement d'algorithme efficace pour la résolution de Problèmes inverses. L'idée de principe est ici, au lieu de calculer la solution exacte f du problème

de calculer une solution approchée 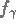. Soit A un opérateur entre des espaces de Hilbert.
Un rôle central dans cette méthode est joué par celui que l'on appelle le Mollifier 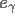et le noyau de reconstruction 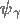. Pour élaborer une méthode de calcul d'inversion approchée, nous choissisons une fonction 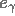et calculons 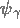comme solution de l'équation

avec A le conjugué de 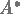. La solution approchée 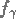correspondant au Mollifier 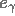choisie est obtenue en appliquant le noyau de reconstruction à droite de g:

Par exemple, en choisissant 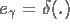, la fonction de Dirac, nous avons comme solution approchée, la solution exacte 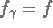, avec la restriction que toutes les équations qui apparaissent lors de la résolution sont solvable de manière unique. Avec un autre choix de 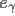, nous obtenons la solution approchée:

Spécialement en vue de la résolution du problème inverse nous devons, pour le choix d'un Mollifier adéquat, avoir en vue les objectifs (concurrentiels) suivants:

1. Une solution 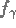unique doit exister et elle doit être stable.
2. La distance 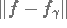doit être aussi petite que possible.
3. Le calcul doit être le plus rapide et prendre le moins de place mémoire possible.

D'autres informations sont à votre disposition sur le fichier Post-Script (355 kByte):