Louis/Maaß/Rieder: Wavelets

Preface
Notation
Introduction

1

The Continuous Wavelet Transform

1. Definition and Elementary Properties
2. Affine Operators
3. Filter Properties
   1. Phasen-Space Representations
   2. Wavelet Transform versus Windowed Fourier Transform
4. Approximation Properties
   1. Asymptotic Behaviour in the Frequency Parameter
   2. Remarks about the Order of Wavelets
5. Decay Behaviour
6. Group-Theoretical Foundations
   1. The Orthogonality Relation for Locally Compact Groups
   2. The Left Transformation
      1. The Wavelet Transform in
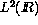
      2. The Windowed Fourier Transform
      3. The Wavelet Transform in
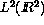
7. Extension of the One-Dimensional Wavelet Transform to Sobolev Spaces

Exercises

2

The Discrete Wavelet Transform

1. Wavelet Frames
   1. Introduction and Definition
   2. The Frame Operator
2. Multiscale Analysis
   1. One-Dimensional Multiscale Analysis
   2. Multidimensional Multiscale Analysis
3. Fast Wavelet Transform
4. One-Dimensional Orthogonal Wavelets
   1. Spline Wavelets
   2. Solving Scaling Equations
   3. Orthogonale Wavelets with Compace Support
   4. Properties of the Daubechies-Wavelets
   5. Biorthogonal Wavelets
   6. Wavelets adapted to Operators
      1. Wavelet-Vaguelette Decompositions
      2. Wavelet-Wavelet Decomposistions
   7. Notes
      1. Wavelets and Derivatives
      2. Wavelets on the Interval
      3. Coiflets
5. Two-Dimensional Orthogonal Wavelets
   1. Tensor Wavelets
   2. Induced Wavelets
   3. Non-Separable Wavelets on the Quincunx Grid

Exercises

3

Applications of the Wavelet Transform

1. Wavelet Analysis of One-Dimensional Signals
   1. Preparations
   2. ECG Analysis
2. Qualitiy Control of Texture
   1. Introduction
   2. Quality measures, Anisotropy and Examples
3. Data Compression in Digital Image Processing
4. Regularization of Inverse Problems
   1. Ill-Posed Problems
   2. Wavelet-Galerkin Methods
      1. Approximation in Sobolev Spaces
      2. A Numerical Example
   3. Mollifier Methods
5. Wavelet-Galerkin Methods for Boundary Value Problems
   1. Two-Point Boundary Value Problems and their Discretization via Galerkin Methods
   2. Wavelet-Galerkin Discretizations
      1. The Wavelet Approximation Space
      2. The Linear System of Equations
6. Schwarz Iterations Based on Wavelet Decompositions
   1. Wavelet-Galerkin Diskretization of the Model Problem
   2. An additive Schwarz Iteration
   3. An Estimate
   4. Generalization of the Schwarz Iteration to Wavelet Packet Spaces
7. An Outlook to Two-Dimensional Boundary Value Problems
   1. A Penality-Fictitious Domain Method
   2. Numerical Aspects and Experiments

Exercises